import casapy
Tutorial of 3c391¶
in bash¶
chmod u+x extractCASAscript.py
python2 extractCASAscript.py 'http://casaguides.nrao.edu/index.php?title=Calibrating_a_VLA_5_GHz_continuum_survey'
python2 extractCASAscript.py 'https://casaguides.nrao.edu/index.php?title=VLA_Continuum_Tutorial_3C391-CASA4.7'
in CASA¶
execfile('CalibratingaVLA5GHzcontinuumsurvey.py')
/Applications/Google Chrome.app/Contents/MacOS/Google Chrome --args --allow-file-access-from-files /Users/brettlv/html/index.html
Flux image and Light curve? errorbar
E and B polarization map Special index map RFI(radio frequency interference) FR(Faraday Rotation)
You may obtain the data set from here:http://casa.nrao.edu/Data/EVLA/3C391/3c391_ctm_mosaic_10s_spw0.ms.tgz(dataset size: 3.1GB). If you wish to start from the very beginning, you may download the dataset from the NRAO Archive: TDEM0001_sb1218006_1.55310.33439732639
Calibrator¶
- J1331+3030 = 3C 286, which will later serve as a calibrator for the visibility amplitudes, i.e., it is assumed to have a precisely known flux density; the spectral bandpass; and the polarization position angle;
- J1822-0938, which will serve as a calibrator for the visibility phases;
- J0319+4130 = 3C 84, which will serve as a polarization calibrator; and
- 3C391 C1–C7, which are 7 fields centered on and surrounding the supernova remnant.
- 4.6GHz and 7.5GHz bandwidth 128MHz
The antennas can be referenced using either convention; antenna='22' would correspond to ea25, whereas antenna='ea22' would correspond to ea22. Note that the antenna numbers in the observer log correspond to the actual antenna names, i.e., the 'ea??' numbers given in listobs
[x] spw id spectrum window
Corrs = [ RR RL LR LL ] clearstat() # This removes any existing table locks generated by flagdata correlation='RR,LL’ correlation='RR,LL' : Plot only the left- and right-handed polarization products. The cross-terms ('RL' and 'LR') will be close to zero for non-polarized sources
The spread of amplitudes in each field is partly due to the difference in gain on each antenna and baseline. Data calibration will take care of much of that scatter.
[x] Export menu
select the Data tab and specify field 0 (source J1331+3030, a.k.a. 3C 286) to display data associated with the amplitude calibrator, then select the Axes tab and change the X-axis to be UVdist(baseline length in meters)
Calibrate the Data:
Note that gaintype='G' assumes the V stokes is zero if not told otherwise, so for the case where the calibrator has significant circular polarization, a model incorporating polarization must be used (this can be set with setjy).
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G0all',xaxis='time',yaxis='phase',poln='R',iteration='antenna',plotrange=[-1,-1,-180,180])
2017-11-14 06:43:16WARNbandpass::::No VLATrDelCorr keyword in the antpos caltable; turning trop delay correction OFF.
Sometimes plotcal will lock a table and/or keep it in the table cache beyond the end of plotting. This can hang up further use of that table, or cause errors if you delete the table outside of CASA and want to re-create it. To deal with that issue, simply close the plotcal GUI using the Quit button when you are done looking at the plot.
All data with the VLA are taken in spectral line mode, even if the science that one is conducting is continuum, and therefore requires a bandpass solution to account for gain variations with frequency
time averaging is 1e10 seconds
Note that for the case of a target with circular polarization gaintype='G ' should only be used if there is a model including the circular polarization, gaintype='G' will assume V=0 in the absence of other information. If you do not have a model containing the circular polarization then gaintype='T' should be used. We know that 3C391 does not have detectable circular polarization so gaintype='G' with no V model is fine.
listobs(vis='3c391_ctm_mosaic_10s_spw0.ms')
plotants(vis='3c391_ctm_mosaic_10s_spw0.ms',figfile='plotants_3c391_antenna_layout.png')
clearstat() # This removes the table lock generated by plotants in script mode
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', flagbackup=True,mode='manual', scan='1')
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', flagbackup=True, mode='manual',antenna='ea13,ea15')
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', mode='quack',quackinterval=10.0, quackmode='beg')
clearstat() # This removes any existing table locks generated by flagdata
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms', selectdata=True, correlation='RR,LL',averagedata=True, avgchannel='64', coloraxis='field')
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='',correlation='RR,LL',timerange='',antenna='ea01',spw='0:31',xaxis='time',yaxis='antenna2',plotrange=[-1,-1,0,26],coloraxis='field')
gencal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.antpos',caltype='antpos')
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms', listmodels=True)
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J1331+3030',standard='Perley-Butler 2013',model='3C286_C.im',usescratch=False,scalebychan=True,spw='')
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms', caltable='3c391_ctm_mosaic_10s_spw0.G0all',
field='0,1,9', refant='ea21', spw='0:27~36',
gaintype='G',calmode='p', solint='int',
minsnr=5, gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G0all',xaxis='time',yaxis='phase',
poln='R',iteration='antenna',plotrange=[-1,-1,-180,180])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G0all',xaxis='time',yaxis='phase',antenna='ea05',
poln='R',iteration='antenna',plotrange=[-1,-1,-180,180],figfile='plotcal_3c391-G0all-phase-R-ea05.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G0all',
xaxis='time', yaxis='phase', poln='L',
iteration='antenna', plotrange=[-1,-1,-180,180])
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms',
flagbackup=True, mode='manual', antenna='ea05')
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms', caltable='3c391_ctm_mosaic_10s_spw0.G0',
field='J1331+3030', refant='ea21', spw='0:27~36', calmode='p', solint='int',
minsnr=5, gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G0',
xaxis='time',yaxis='phase',poln='R',field='J1331+3030',iteration='antenna',
plotrange=[-1,-1,-180,180],timerange='08:02:00~08:17:00')
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.K0',
field='J1331+3030',refant='ea21',spw='0:5~58',gaintype='K',
solint='inf',combine='scan',minsnr=5,
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.G0'])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.K0',xaxis='antenna',yaxis='delay',
figfile='plotcal_3c391-K0-delay.png')
Calibration¶
Bandpass calibration¶
bandpass(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.B0',
field='J1331+3030',spw='',refant='ea21',combine='scan',
solint='inf',bandtype='B',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.G0',
'3c391_ctm_mosaic_10s_spw0.K0'])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.B0',poln='R',xaxis='chan',yaxis='amp',field='J1331+3030',subplot=221,iteration='antenna',figfile='plotcal_3c391_3c286_B0_R_amp.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.B0',poln='L',xaxis='chan',yaxis='amp',field='J1331+3030',subplot=221,iteration='antenna',figfile='plotcal_3c391_3c286_B0_L_amp.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.B0',poln='R',xaxis='chan',yaxis='phase',field='J1331+3030',subplot=221,iteration='antenna',plotrange=[-1,-1,-180,180],figfile='plotcal_3c391_3c286_B0_R_phase.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.B0',poln='L',xaxis='chan',yaxis='phase',field='J1331+3030',subplot=221,iteration='antenna',plotrange=[-1,-1,-180,180],figfile='plotcal_3c391_3c286_B0_L_phase.png')
Gain calibration¶
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.G1',field='J1331+3030',spw='0:5~58',refant='ea21',solint='inf',gaintype='G',calmode='ap',solnorm=False,gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0'],interp=['linear','linear','nearest'])
delete combine='scan'¶
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.G1',field='J1822-0938',spw='0:5~58',refant='ea21',solint='inf',gaintype='G',calmode='ap',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0'],append=True)
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.G1',field='J0319+4130',spw='0:5~58',refant='ea21',solint='inf',gaintype='G',calmode='ap',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0'],append=True)
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='phase',poln='R',plotrange=[-1,-1,-180,180],figfile='plotcal_3c391_G1_phase_R.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='phase',poln='L',plotrange=[-1,-1,-180,180],figfile='plotcal_3c391_G1_phase_L.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='amp',poln='R',figfile='plotcal_3c391_G1_amp_R.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='amp',poln='L',figfile='plotcal_3c391_G1_amp_L.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='phase',poln='/',plotrange=[-1,-1,-180,180],figfile='plotcal_3c391_G1_phase_rat.png')
Polarization Calibration¶
import math
from math import log,pi
alpha=log(7.53261/7.6677)/log(4663.0/4536.0)
i0=7.6677
c0=0.112
d0=33*pi/180
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J1331+3030',standard='manual',spw='0',fluxdensity=[i0,0,0,0],spix=[alpha,0],reffreq='4536.0MHz',polindex=[c0,0],polangle=[d0,0],scalebychan=True,usescratch=False)
{'0': {'0': {'fluxd': array([ 7.6677 , 0.34929827, 0.78453676, 0. ])},
'fieldName': 'J1331+3030'},
'format': "{field Id: {spw Id: {fluxd: [I,Q,U,V] in Jy}, 'fieldName':field name }}"}
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='RR',timerange='08:02:00~08:17:00',antenna='ea01&ea02',xaxis='channel',yaxis='amp',ydatacolumn='model',plotfile='plotms_3c391_model_amp_RR.png',overwrite=True)
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='RR',timerange='08:02:00~08:17:00',antenna='ea01&ea02',xaxis='channel',yaxis='phase',ydatacolumn='model',plotfile='plotms_3c391_model_phase_RR.png',overwrite=True)
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='RL',timerange='08:02:00~08:17:00',antenna='ea01&ea02',xaxis='channel',yaxis='amp',ydatacolumn='model',plotrange=[-1,-1,-180,180],plotfile='plotms_3c391_model_amp_RL.png',overwrite=True)
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='RL',timerange='08:02:00~08:17:00',antenna='ea01&ea02',xaxis='channel',yaxis='phase',ydatacolumn='model',plotrange=[-1,-1,-180,180],plotfile='plotms_3c391_model_phase_RL.png',overwrite=True)
name='3c391_ctm_mosaic_10s_spw0'
Solve cross-hand delay¶
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.Kcross',field='J1331+3030',spw='0:5~58',gaintype='KCROSS',solint='inf',combine='scan',refant='ea21',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0','3c391_ctm_mosaic_10s_spw0.G1'],gainfield=['','','J1331+3030'],parang=True)
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.Kcross',xaxis='antenna',yaxis='delay',figfile='plotcal_3c391_Kcross_delay.png')
Solve leakage terms¶
polcal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.D1',field='J0319+4130',spw='0:5~58',refant='ea21',poltype='Df',solint='inf',combine='scan',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0','3c391_ctm_mosaic_10s_spw0.G1','3c391_ctm_mosaic_10s_spw0.Kcross'],gainfield=['','','','J0319+4130',''])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.D1',xaxis='chan',yaxis='amp',spw='',field='',iteration='antenna')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.D1',xaxis='chan',yaxis='phase',spw='',field='',iteration='antenna',plotrange=[-1,-1,-180,180])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.D1',xaxis='antenna',yaxis='amp',figfile='plotcal_3c391_D1.png')
polcal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.D2',field='J1822-0938',spw='0:5~58',refant='ea21',poltype='Df+QU',solint='inf',combine='scan',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0','3c391_ctm_mosaic_10s_spw0.G1','3c391_ctm_mosaic_10s_spw0.Kcross'],gainfield=['','','','J1822-0938',''])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.D2',xaxis='antenna',yaxis='amp',figfile='plotcal_3c391_D2.png')
Solve R_L polarization angle¶
polcal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.X1',field='J1331+3030',poltype='Xf',solint='inf',combine='scan',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0','3c391_ctm_mosaic_10s_spw0.G1','3c391_ctm_mosaic_10s_spw0.Kcross','3c391_ctm_mosaic_10s_spw0.D2'],gainfield=['','','','J1331+3030','',''])
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.X1',xaxis='chan',yaxis='phase',figfile='plotcal_3c391_X1.png')
Scale amp gains¶
myscale_3c391=fluxscale(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.G1',fluxtable='3c391_ctm_mosaic_10s_spw0.fluxscale1',reference=['J1331+3030'],transfer=['J1822-0938,J0319+4130'],incremental=False)
myscale_3c391['1']
myscale_3c391['9']
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.fluxscale1',xaxis='time',yaxis='amp',poln='R',figfile='plotcal_3c391_fluxscale_amp_R.png')
plotcal(caltable='3c391_ctm_mosaic_10s_spw0.fluxscale1',xaxis='time',yaxis='amp',poln='L',figfile='plotcal_3c391_fluxscale_amp_L.png')
Apply calibration¶
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J1331+3030',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.fluxscale1','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0','3c391_ctm_mosaic_10s_spw0.Kcross','3c391_ctm_mosaic_10s_spw0.D2','3c391_ctm_mosaic_10s_spw0.X1'],gainfield=['','J1331+3030','','','','',''],interp=['','nearest','','','','',''],calwt=[False],parang=True)
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J0319+4130',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.fluxscale1','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0','3c391_ctm_mosaic_10s_spw0.Kcross','3c391_ctm_mosaic_10s_spw0.D2','3c391_ctm_mosaic_10s_spw0.X1'],gainfield=['','J0319+4130','','','','',''],interp=['','nearest','','','','',''],calwt=[False],parang=True)
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J1822-0938',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.fluxscale1','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0','3c391_ctm_mosaic_10s_spw0.Kcross','3c391_ctm_mosaic_10s_spw0.D2','3c391_ctm_mosaic_10s_spw0.X1'],gainfield=['','J1822-0938','','','','',''],interp=['','nearest','','','','',''],calwt=[False],parang=True)
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',field='2~8',gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.fluxscale1','3c391_ctm_mosaic_10s_spw0.K0','3c391_ctm_mosaic_10s_spw0.B0','3c391_ctm_mosaic_10s_spw0.Kcross','3c391_ctm_mosaic_10s_spw0.D2','3c391_ctm_mosaic_10s_spw0.X1'],gainfield=['','J1822-0938','','','','',''],interp=['','linear','','','','',''],calwt=[False],parang=True)
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='',timerange='08:02:00~08:17:00',antenna='',avgtime='60',xaxis='channel',yaxis='amp',ydatacolumn='corrected',coloraxis='corr',plotfile='plotms_3c391_fld0_corrected_amp.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='',timerange='08:02:00~08:17:00',antenna='',avgtime='60',xaxis='channel',yaxis='phase',ydatacolumn='corrected',coloraxis='corr',plotrange=[-1,-1,-180,180],plotfile='plotms_3c391_fld0_corrected_phase.png',overwrite=True)
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='1',correlation='RR,LL',timerange='',antenna='',avgtime='60',xaxis='channel',yaxis='amp',ydatacolumn='corrected',coloraxis='corr',plotfile='plotms_3c391_fld1_corrected_amp.png',overwrite=True)
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='1',correlation='RR,LL',timerange='',antenna='',avgtime='60',xaxis='channel',yaxis='phase',plotrange=[-1,-1,-180,180],ydatacolumn='corrected',coloraxis='corr',plotfile='plotms_3c391_fld1_corrected_phase.png',overwrite=True)
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='1',correlation='RR,LL',timerange='',antenna='',avgtime='60',xaxis='phase',xdatacolumn='corrected',yaxis='amp',plotrange=[-180,180,0,3],ydatacolumn='corrected',coloraxis='corr',plotfile='plotms_3c391_fld1_corrected_ampvsphase.png',overwrite=True)
split(vis='3c391_ctm_mosaic_10s_spw0.ms',outputvis='3c391_ctm_mosaic_spw0.ms',datacolumn='corrected',field='2~8')
Initial image¶
plotms(vis='3c391_ctm_mosaic_spw0.ms',field='0',correlation='RR',avgtime='30',xaxis='uvwave',yaxis='amp',ydatacolumn='data',plotfile='plotms_3c391_mosaic0_uvwave.png',overwrite=True)
clean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_I',field='',spw='',mode='mfs',niter=5000,gain=0.1,threshold='1.0mJy',psfmode='clark',imagermode='mosaic',ftmachine='mosaic',multiscale=[0],interactive=True,imsize=[480,480],cell=['2.5arcsec','2.5arcsec'],stokes='I',weighting='briggs',robust=0.5,usescratch=False)
viewer('3c391_ctm_spw0_I.image')
clean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_IQUV',field='',spw='',mode='mfs',niter=25000,gain=0.1,threshold='1.0mJy',psfmode='clarkstokes',imagermode='mosaic',ftmachine='mosaic',multiscale=[0,6,18,54],smallscalebias=0.9,interactive=True,imsize=[480,480],cell=['2.5arcsec','2.5arcsec'],stokes='IQUV',weighting='briggs',robust=0.5,pbcor=False,usescratch=False)
viewer('3c391_ctm_spw0_IQUV.image')
impbcor(imagename='3c391_ctm_spw0_IQUV.image',pbimage='3c391_ctm_spw0_IQUV.flux',outfile='3c391_ctm_spw0_IQUV.pbcorimage')
mystat=imstat(imagename='3c391_ctm_spw0_IQUV.pbcorimage',stokes='')
{'blc': array([0, 0, 0, 0], dtype=int32),
'blcf': '18:50:04.251, -01.05.40.567, I, 4.59901e+09Hz',
'max': array([ 0.15470561]),
'maxpos': array([288, 256, 0, 0], dtype=int32),
'maxposf': '18:49:16.243, -00.55.00.579, I, 4.59901e+09Hz',
'mean': array([ 0.00092122]),
'medabsdevmed': array([ 0.00018971]),
'median': array([ 1.51867052e-05]),
'min': array([-0.00640078]),
'minpos': array([279, 430, 0, 0], dtype=int32),
'minposf': '18:49:17.743, -00.47.45.579, I, 4.59901e+09Hz',
'npts': array([ 483720.]),
'q1': array([-0.00016487]),
'q3': array([ 0.0002171]),
'quartile': array([ 0.00038197]),
'rms': array([ 0.00610539]),
'sigma': array([ 0.0060355]),
'sum': array([ 445.61365631]),
'sumsq': array([ 18.03106503]),
'trc': array([479, 479, 3, 0], dtype=int32),
'trcf': '18:48:44.407, -00.45.43.065, V, 4.59901e+09Hz'}
mystat['max'][0]
The three most basic analyses are to determine the peak brightness, the flux density, and the image noise level.
viewer('3c391_ctm_spw0_IQUV.pbcorimage')
(3c391_ctm_spw0_IQUV.pbcorimage)
Stokes Velocity Frame Doppler Frequency
I -42.9832km/s LSRK RADIO 4.59901e+09
BrightnessUnit BeamArea Npts Sum FluxDensity
Jy/beam 45.1039 26989 2.228439e+02 4.940680e+00
Mean Rms Std dev Minimum Maximum
8.256841e-03 2.126741e-02 1.959953e-02 -1.374126e-02 1.509379e-01
region count
1
-----------
(3c391_ctm_spw0_IQUV.pbcorimage)
Stokes Velocity Frame Doppler Frequency
I -42.9832km/s LSRK RADIO 4.59901e+09
BrightnessUnit BeamArea Npts Sum FluxDensity
Jy/beam 45.1039 55029 4.297441e+02 9.527872e+00
Mean Rms Std dev Minimum Maximum
7.809411e-03 1.802475e-02 1.624529e-02 -3.866892e-03 1.547056e-01
region count
1
<font color=red>流量(Jy) </font> 4.94(less iteration)/9.52(more iteration)
From casa cookbook¶
Listed Parameters are Stokes, and the displayed channel Velocity with the associated Frame, Doppler and Frequency value. Sum, Mean, Rms, Std Deviation, Minimum, and Maximum value refer to those in the selected region and has the units as specified in BrightnessUnit. Npts is the number of pixels in the region, and BeamArea the beam size in pixels. FluxDensity is in Jy if the image is in Jy/beam. This is an easy way to copy and paste the statistical data to a program outside of CASA for further use.
Taking the RMS of the signal-free portion of an image or cube is a good way to estimate the noise. Contrasting this number with the maximum of the image gives an estimate of the dynamic range of the image. The FluxDensity measurement gives a way to use the viewer to do very basic photometry.
By contrast, for the rms noise level, one can load the original (un-pbcor) image:
# In CASA
viewer('3c391_ctm_spw0_IQUV.image')and to exclude the source's emission to the extent possible as shown in figure 30, as the source's emission will bias the estimated noise level high. Likewise, one should avoid the clean bowl around the source emission.
(3c391_ctm_spw0_IQUV.image)
Stokes Velocity Frame Doppler Frequency
I -42.9832km/s LSRK RADIO 4.59901e+09
BrightnessUnit BeamArea Npts Sum FluxDensity
Jy/beam 45.1039 24071 3.914005e+02 8.677756e+00
Mean Rms Std dev Minimum Maximum
1.626025e-02 2.509083e-02 1.910940e-02 -2.093949e-03 1.404008e-01
region count
1
-----------------
(3c391_ctm_spw0_IQUV.image)
Stokes Velocity Frame Doppler Frequency
I -42.9832km/s LSRK RADIO 4.59901e+09
BrightnessUnit BeamArea Npts Sum FluxDensity
Jy/beam 45.1039 34920 -5.131547e+00 -1.137717e-01
Mean Rms Std dev Minimum Maximum
-1.469515e-04 5.875222e-04 5.688558e-04 -2.366036e-03 6.803005e-03
region count
1
lamda=30/4.6 #cm
D=lamda*16000/100#baseline m
D
23000/45*0.6/1000
Construct polarization intensity and angle image¶
imsubimage(imagename='3c391_ctm_spw0_IQUV.image',outfile='3c391_ctm_spw0.I',stokes='I')
imsubimage(imagename='3c391_ctm_spw0_IQUV.image',outfile='3c391_ctm_spw0.Q',stokes='Q')
imsubimage(imagename='3c391_ctm_spw0_IQUV.image',outfile='3c391_ctm_spw0.U',stokes='U')
imsubimage(imagename='3c391_ctm_spw0_IQUV.image',outfile='3c391_ctm_spw0.V',stokes='V')
imsubimage(imagename='3c391_ctm_spw0_IQUV.pbcorimage',outfile='3c391_ctm_spw0.pbcorI',stokes='I')
Few celestial sources, with the notable exception of masers, are expected to show circular polarization. Terrestrial and satellite sources, however, are often highly circularly polarized. The V image is therefore often worth forming because any V emission could be indicative of unflagged RFI within the data (or problems with the calibration!).
immath(outfile='3c391_ctm_spw0.P',mode='poli',imagename=['3c391_ctm_spw0.Q','3c391_ctm_spw0.U'],sigma='0.0Jy/beam')
immath(outfile='3c391_ctm_spw0.P_unbias',mode='poli',imagename=['3c391_ctm_spw0.Q','3c391_ctm_spw0.U'],sigma='0.000041Jy/beam')
imsubimage(imagename='3c391_ctm_spw0_IQUV.flux',outfile='3c391_ctm_spw0.Qflux',stokes='Q')
immath(outfile='3c391_ctm_spw0.pbcorP',mode='evalexpr',imagename=['3c391_ctm_spw0.P_unbias','3c391_ctm_spw0.Qflux'],expr="IM0[IM1>0.2]/IM1")
immath(outfile='3c391_ctm_spw0.X',mode='pola',imagename=['3c391_ctm_spw0.Q','3c391_ctm_spw0.U'],polithresh='0.2mJy/beam')
immath(outfile='3c391_ctm_spw0.F',mode='evalexpr',imagename=['3c391_ctm_spw0.I','3c391_ctm_spw0.Q','3c391_ctm_spw0.U'],expr='sqrt((IM1^2+IM2^2)/IM0[IM0>1.2e-3]^2)')
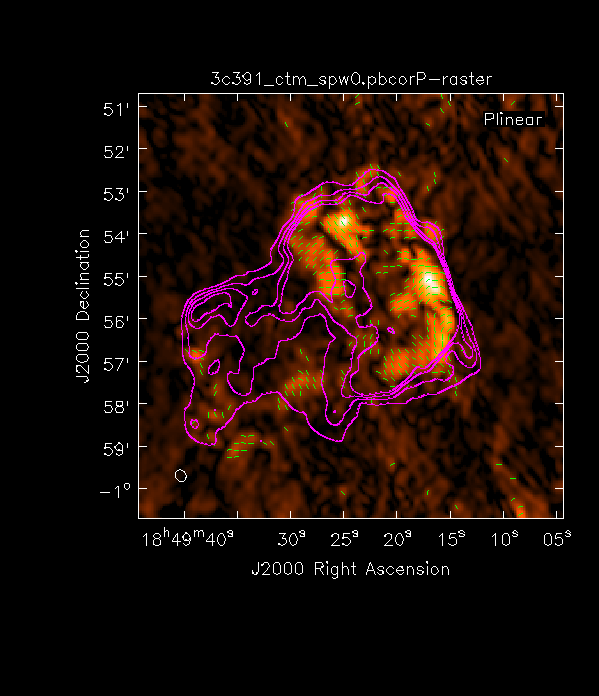
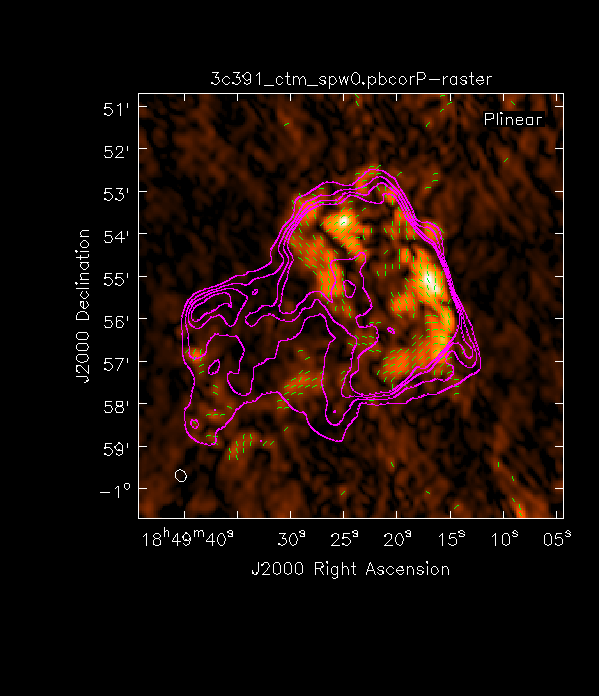
viewer('3c391_ctm_spw0.pbcorP')
viewer('3c391_ctm_spw0.pbcorP')
- This will look terrible because the Data Range is set to [-1 1], you can change the Data Range manually by clicking on the wrench icon to open a Data Display Options GUI ([-6.224e-07, 0.002687] seemed to work well).
- Next, load the pb-corrected total intensity image as a contour image. In the viewer panel, press the Open icon (the leftmost button in the top row of icons in the viewer). This will bring up a Load Data GUI showing all images and MS in the current directory.
- Select the total intensity image (3c391_ctm_spw0.pbcorI) and click the Contour Map button on the right hand side.
- Finally, load the polarization position angle image (3c391_ctm_spw0.X) as a vector map.
While we set the parameter polithresh when we created the position angle (X) image, a digression here is instructive in the use of Lattice Expression Language (LEL) Expressions.
'3c391_ctm_spw0.X'['3c391_ctm_spw0.pbcorP'>0.0004]
The polarization position angle as calculated is the electric vector position angle (EVPA).¶
If we are interested in the orientation of the magnetic field, then for <font color=red>an optically thin source </font>, the magnetic field orientation is perpendicular to the EVPA, so we must rotate the vectors by $90^{\circ}$
Spectral index image¶
index=$\log(S_{\nu_1}/S_{\nu_2})/\log(\nu_1/\nu_2)$¶
is a useful analytical tool that can convey information about the emission mechanism, the optical depth of the source or the underlying energy distribution of synchrotron-radiating electrons
Self Calibration¶
Self-calibration is the process of using an existing model, often constructed from imaging the data itself, provided that sufficient visibility data have been obtained. This is essentially always the case with data: the system of equations is wildly over-constrained for the number of unknowns.
More specifically, the observed visibility data on the i-j baseline can be modeled as
$V'_{ij} = G_i G^*_j V_{ij}$ where $G_i$ is the complex gain for the $i^{\mathrm{th}}$ antenna and $V_{ij}$ is the true visibility. For an array of N antennas, at any given instant, there are N(N-1)/2 visibility data, but only N gain factors. For an array with a reasonable number of antennas, N >~ 8, solutions to this set of coupled equations converge quickly.
delmod('3c391_ctm_mosaic_spw0.ms')#We first use delmod on the MS to get rid of the previous polarized model.
$\log(S_{\nu_1}/S_{\nu_2})/\log(\nu_1/\nu_2)$
clean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_ms_I',field='',spw='',mode='mfs',niter=25000,gain=0.1,threshold='1mJy',psfmode='clark',imagermode='mosaic',ftmachine='mosaic',multiscale=[0,6,18,54],smallscalebias=0.9,interactive=True,imsize=[480,480],cell=['2.5arcsec','2.5arcsec'],stokes='I',weighting='briggs',robust=0.5,usescratch=False)
gaincal(vis='3c391_ctm_mosaic_spw0.ms',caltable='3c391_ctm_mosaic_spw0.selfcal1',field='',spw='',selectdata=False,solint='30s',refant='ea21',minblperant=4,minsnr=3,gaintype='G',calmode='p',append=False)
applycal(vis='3c391_ctm_mosaic_spw0.ms',field='',spw='',selectdata=False,gaintable=['3c391_ctm_mosaic_spw0.selfcal1'],gainfield=[''],interp=['nearest'],calwt=[False],applymode='calflag')
viewer('3c391_ctm_spw0_ms_I.image')
Note that for the case of a target with circular polarization gaintype='G ' should only be used if there is a model including the circular polarization, gaintype='G' will assume V=0 in the absence of other information.¶
If you do not have a model containing the circular polarization then gaintype='T' should be used. We know that 3C391 does not have detectable circular polarization so gaintype='G' with no V model is fine.
clean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_IQUV_selfcal1',field='',spw='',mode='mfs',niter=25000,gain=0.1,threshold='1mJy',psfmode='clarkstokes',imagermode='mosaic',ftmachine='mosaic',multiscale=[0,6,18,54],smallscalebias=0.9,interactive=True,imsize=[480,480],cell=['2.5arcsec','2.5arcsec'],stokes='IQUV',weighting='briggs',robust=0.5,usescratch=False)
plotms(vis='3c391_ctm_mosaic_spw0.ms')
viewer('3c391_ctm_spw0_IQUV_selfcal1')
Commonly, this self-cal procedure is applied multiple times. The number of iterations is determined by a combination of the data quality and number of antennas in the array, the structure of the source, the extent to which the original self-calibration assumptions are valid, and the user's patience. With reference to the original self-calibration equation above, if the observed visibility data cannot be modeled well by this equation, no amount of self-calibration will help.
End and Comments¶
here are several general comments or guidelines:
- An I-only image/model must be made for each new round of self-cal, rather than the IQUV image shown above.
- Bookkeeping is important! Suppose one conducts 9 iterations of self-calibration. Will it be possible to remember one month later (or maybe even one week later!) which set of gain corrections and images are which? In the example above, the descriptor 'selfcal1' is attached to various files to help keep straight which is what. Successive iterations of self-cal could then be 'selfcal2' , 'selfcal3' , etc.
- Care is required in the setting of imagename. If one has an image that already exists, CASA will continue cleaning it (if it can), which is almost certainly not what one wants during self-calibration. Rather one wants a unique imagename for each pass of self-calibration.
- A common metric for self-calibration is whether the image dynamic range (= max/rms) has improved. An improvement of 10% is quite acceptable.
- Be careful when making images and setting clean regions or masks. Self-calibration assumes that the model is perfect. If one cleans a noise bump, self-calibration will quite happily try to adjust the gains so that the CORRECTED_DATA describe a source at the location of the noise bump. As the author demonstrated to himself during the writing of his thesis, it is quite possible to take completely noisy data and manufacture a source. It is far better to exclude some feature of a source or a weak source from initial cleaning and conduct another round of self-calibration than to create an artificial source. If a real source is excluded from initial cleaning, it will continue to be present in subsequent iterations of self-calibration; if it's not a real source, one probably isn't interested in it anyway.
- Start self-calibration with phase-only solutions (parameter calmode='p' in gaincal). As discussed in the High Dynamic Range Imaging lecture, a phase error of 20 deg is as bad as an amplitude error of 10%.
- In initial rounds of self-calibration, consider solution intervals longer than the nominal sampling time (parameter solint in gaincal) and/or lower signal-to-noise ratio thresholds (parameter minsnr in gaincal). Depending upon the frequency and configuration and fidelity of the model image, it can be quite reasonable to start with solint='30s' or solint='60s' and/or minsnr=3 (or even lower). One might also want to consider specifying a uvrange, if, for example, the field has structure on large scales (small -) that is not well represented by the current image.
- The task applycal will flag data with no good calibration solutions. During the initial self-calibration steps, this flagging may be excessive. If so, one can restore the flags to the state right before running applycal by using the task flagmanager.
- You can track the agreement between the DATA, CORRECTED_DATA, and MODEL in plotms. The options in Axes tab allows one to select which column is to be plotted. If the MODEL agrees well with the CORRECTED_DATA, one can use shorter solint and/or higher minsnr values.
- You should consider examining the solutions from gaincal by using plotcal in order to assure that the corrections are sensible. Smoothly varying phases are good, jumps are usually not. (However, because the phases are often plotted ±180 degrees, there can be apparent jumps if the phases are very near +180 deg or −180 deg.)
- In the case of a mosaic, such as here, one should also verify that the solutions are of equal quality for all of the fields.